3. Codes

3.1 Introduction

An N-bit register can assume one of 2^N configurations or states. Associated with each of these states is a binary word of length N, X_j,j=1,2^N. The set of all X_j comprises the register set R_N. Note that by its definition this is a complete set, ie it consists of every possible N-bit word.

A code is a generalized function defined on R_N or a subset which defines a correspondence between each word of the set or subset and a desired item. Thus the register set has the capacity to code for 2^N items. Several points are worth emphasizing at this juncture. A binary word is a mathematical entity in its own right, but it has no implied interpretation. A word only has meaning within the context of a code. Codes are arbitrary and no one code has precedence. A given binary word may be generated based upon one code but interpreted differently within the context of a second.

As a concrete example consider a small company dealing in stone which has an inventory of 8 different types. It is then possible to represent the inventory using R₃. Consider the accompanying table which lists the types and a possible code.

Notice that the MSB is used to distinguish between type while the two LSBs designate colour. In general the bits of a word may be subdivided into groups, each group comprising a field. Thus in this simple example, bit 1 would be the type field and bits 2 and 3 the colour field.

It is important to re-emphasize that within the context of this code, no other interpretation of the words in the set is possible.

3.2 Binary Code for Unsigned Integers

While the above code for stones is highly specialized, a much more common and useful code application is in the representation of numerical information. The simplest form of numerical information is that of unsigned integers 0,1,2,3,·····. The most common code used to represent these with a register set, referred to briefly as the binary code, is also one consistent with the general mathematical representation employing an arbitrary basis, specialized in this instance to base 2. The relationship between a binary word X={x_i,i=1,N} and the integer in its normal base 10 representation I₁₀(X) is given by

The relationship given in Equation (3.1) is consistent with normal number theory except that the base b replaces 2, and the variable x can assume one of b values. Notice that the integers which may be represented in the binary code using R_N range from 0 to 2^N-1. The situation for the case of N = 3 is compared with the code for stones in the following table.

A given word now has two interpretations associated with it so that it is extremely important to clearly define the relevant code when the word is employed. Note that it is also possible to translate between codes. Thus a digital system might send a message based upon the binary code employing the integer 5, which would be represented in a register by the word 101. This message could then be transmitted to a second digital system which employing the stone classification code would interpret the message, X=101, as signifying black granite. Similarly transmission of the word 001 in the reverse direction would result in the translation from buff sandstone to the integer one.

Two frequently employed number bases are b=8, referred to as octal, and b=16, referred to as hexadecimal. These two systems are popular, not to represent integers so much as to provide a convenient compact notation for denoting a binary word. Formally they may be thought to arise from octal and hexadecimal physical elements characterized by having 8 and 16 states respectively. Consider the 6-bit binary word X=101111. This can be decomposed into two consecutive 3-bit words 100 111 which can then be translated according to the standard binary integer code into 47₈. The latter can be thought of as arising from a system of two octal elements, an octal register of length two. The states of each octal element are then designated by the symbols 0 to 7. Both the binary and octal words represent the decimal number 39 in the standard number representation, but this may in fact be irrelevant. A quite different code might be in effect so that the 6-bit word might represent something quite different. Nevertheless, it could still be described succinctly by 47₈. Expansion from the octal word to the corresponding binary word is simply achieved by substituting the corresponding three bits for each octal digit. A standard word length of 8, corresponding to a byte, is not divisible by 3. An octal condensation is still quite possible, and the range for a byte would be from 000 to 377, since the binary word decomposes into one 2-bit word followed by two 3-bit words.

A byte may be evenly decomposed into two four bit words each of which then is isomorphic with one of the sixteen states of a hexadecimal element. These states are designated with the symbols 0 to 9, followed by A,B,C,D,E,and F. Again, a hexadecimal word of length 2 is a compact notation for a binary word of length 8. For example, E9 is a short form for 11101001. The 4 MSB, 1110 are the binary code for 14, or E, while the 4 LSB code for 9. Again both are in fact the standard code for the decimal integer 233, but this may or may not be important. Whatever code is actually in effect, E9 is a compact representation of the binary word X=11101001 of length 8.

3.3 Gray's Code

This code, also referred to as the reflected code, is a variation of the standard code with which it is compared for N=3 in the following table.

The general approach to constructing this code is as follows. Note that for both codes the lower half of the integers are represented by words with an MSB of 0, while the words representing the upper half have MSB=1. In the standard binary code the remaining bits in the upper half are repeated in the same order as for the lower half. In Gray's code the remaining bits are reflected about the midpoint. Thus for N=1 there is only 0 and 1. For N=2 we have 00,01,11,10 where the least significant bit appears in the order 0,1,1,0 corresponding to the reverse, or reflected, order for the second two words. This process is then repeated to extend the scheme to words of greater length. Thus to construct the code for N=4, the eight words in the above table would be written as above. These would then be followed by eight words written in the reverse order. An MSB of 0 would then be attached ahead of the first eight 3 bit words to create 4 bit words. Similarly an MSB of 1 would be attached to the second eight words, completing the code.

Gray's code certainly seems unnecessarily complicated and one might well ask why on earth it was devised. A close examination of the code reveals that in cycling through the integers in either increasing or decreasing order the distance between consecutive code words is always 1. This is unlike the standard code where, for example, the distance between the words coding for integers 3 and 4 is 3, so that three elements in the register must change state in this single step of the cycle. It is technically advantageous to avoid this type of situation, although normally difficult to do so, since in many cases processes do not cycle in an orderly fashion through the integers being represented. A common situation in which such cycling does occur is rotational motion. If sectors of angle 2p/2^N are used to describe the orientation and numbered consecutively from 0 to 2^N-1 then the process will always proceed from its initial state to its final state by cycling through the integers consecutively. Note that the sectors could just as easily have been designated 1 to 2^N, the nomenclature used in the table merely facilitating comparison with the standard binary code. Again it must be emphasized that the table illustrates that no unique meaning can be given to a binary word unless a code is defined, and that the interpretation of a given word depends critically upon the code used. Thus 100 represents the integer 4 in the binary code and 7 in Gray's code.

3.4 Binary Code for Real Numbers

In order to represent positive real numbers, a field structure is introduced. The word is divided into an integer field comprised of the N-M most significant bits and a fractional field consisting of the remaining M least significant bits. The coding relationship is consistent with general number theory so that the binary word X={x_i,i=1,N} codes for the real decimal number R₁₀(X) given by

The above equation can be generalized to any base b simply by replacing 2 by b. By convention the partition of the word into its two fields is indicated by a period, familiar for b=10 as the decimal point. Thus if a byte is decomposed to have a fractional field of length three it would generally be written x₁x₂x₃x₄x₅.x₆x₇x₈ and the period plays the role of a binary point.

To convert a positive decimal number to its binary representation, repeated divisions by the base 2 of the integer part and repeated multiplications by 2 of the fractional part are used. Consider for example a decimal number which is represented by N=6, M=3 so that

Division of the integer part by two gives 2x₁+x₂ with a remainder, the fractional part of the quotient, of x₃. Division of 2x₁+x₂ gives x₁ with a remainder of x₂. The final remainder is then x₁. Thus the successive remainders produced by repeated division correspond to the bits in the reverse order, ie beginning with the LSB of the integer field and ending with the MSB. Multiplication of the fractional part by 2 gives a product of x₄+x₅/2+x₆/4, with integer part being the MSB of the fractional field, x₄. A second multiplication of the fractional part gives x₅+x₆/2 with integer part x₅ and a final multiplication yields a product with integer part x₆. In summary, repeated division of the integer part of a decimal number produces at each stage a quotient with fractional part equal to a corresponding bit in the integer field of the binary representation, beginning with the LSB of the field and ending with the MSB of the entire word. Repeated multiplication of the fractional part of a decimal number produces at each stage a product, the integer part of which corresponds to a bit of the fractional field of the binary representation, beginning with the MSB of the field and ending with the LSB of the entire word.

In the example of N=6, M=3 above, notice that all real numbers with value less than 1/8, or 0.125, will be represented by the binary word consisting of x_i=0, i=1,6, ie F. Using Eqn (3.3) this word would be translated as the decimal number 0 according to the code definition of Eqn(3.2). A situation in which a finite number produces a representation of 0 in the binary code is referred to as an underflow. Similarly, the maximum number is represented by the word of weight 6, U, corresponding to the decimal number 7.875. Representation of numbers greater than this maximum leads to the error condition referred to as an overflow.

Because the register set R₆ has only 64 members, only 64 distinct quantities may be represented. Clearly the real numbers between any interval form an infinite set. In the scheme being discussed, any two real numbers which differ by less than 0.125 would be represented by the same six-bit binary word, and hence would become indistinguishable. Thus any binary representation is characterized by a finite precision as well as a finite range. The range may be extended, and the precision improved by increasing the word length, but it must be realized that both will always remain finite.

3.5 Two's Complement Code

For the codes discussed so far no provision has been made for the representation of negative numbers. Different approaches are taken to this problem. The most useful arithmetically is the twos complement code, based upon the twos complement operation to be defined shortly. Before doing so it must be emphasized that the code is NOT the operation, but makes use of it. Thus for example, representing the decimal number 5 in the twos complement code is not the same as performing the twos complement operation on the binary word representing 5.

Before defining the operation it is useful to consider some properties of N-bit words. First consider the word obtained from summing a word X with its complement. Thus givenand the sum of any logical variable with its complement is 1, it follows that

where U is the word of weight N, ie all bits equal 1. This word also has the property that

where the left hand side is to be interpreted as the addition of the binary word of unit weight with LSB=1, and F is the word of weight 0 and codes for the decimal number 0 in either the standard binary code for integers or real numbers. It is important to note that properties (3.5) and (3.6) are code independent.

The two's complement operation consists of complementing the word followed by the addition of the word of weight 1 with LSB=1. As an example, for N=8, this word would be 00000001. Designating the twos complement of X by C₂(X) this can be written as

It then follows from Eqn(3.5) and (3.6) that

Thus addition of any word of the register set under consideration to its two's complement generates the word of weight 0 which codes for the decimal number 0 in the standard numerical codes. It is natural therefore to associate a word and its twos complement with codes for decimal numbers of the same magnitude and opposite sign. As a specific example consider the twos complement code for signed integers using R₃ tabulated below.

The code is constructed as follows. The register set R_N is decomposed into two subsets each containing 1/2 the words in the register set. The first, R_N(0) consists of the set of all N-bit words with MSB=0, and the second, R_N(1), the set of all N-bit words with MSB=1.

Note that both subsets are in fact isomorphic to R_N-1. By convention the members of R_N(0) are used in a standard code for positive decimal numbers. To each word in R_N(0) coding for a non-zero decimal number there is the corresponding twos complement in R_N(1) which is assigned to be the code for the negative value. Since the arithmetic sum produces the word coding for 0, this is internally consistent with normal arithmetic.

There is one word in each subset which is its own two's complement and hence does not have a correspondence. For R_N(0) this is the word of weight 0, designated F. Since this word codes for the decimal number 0, and -0 has no distinct meaning this is also in accord with normal arithmetic. The word in the subset R_N(1) having this property is the word of weight one. This has the structure of MSB=1 and all remaining bits zero. In the example of N=3 it is the entry 100. Its value is assigned so as to ensure arithmetic consistency under addition. Thus 100+001=101. Since 001 and 101 code for the decimal numbers 1 and -3 in the twos complement representation of signed integers the code assigned to 100 is -4. Notice that the decomposition of the register set into the two subsets described leads to a field structure in which the MSB is a one bit field conveying sign information, ie MSB=0 indicates a code word for a positive number and MSB=1 indicates the word codes a negative number.

The twos complement code is equally applicable to real number representations. For example if N=3,M=1 the decimal numbers represented corresponding to the three bit words in the order presented above are, 0.0,0.5,1.0,1.5,-2.0,-1.5,-1.0,-0.5.

3.6 Floating Point Code

As mentioned above limitations on both the range and precision with which real numbers are represented is imposed by the finite word length. The floating point code is an approach analogous to the decimal representation of say, 125.35 as 1.2535x10². The word is decomposed into three fields of length 1, P and M=N-P-1. The first is a one bit field corresponding to the MSB and conveys sign information in the same manner as the twos complement code. The second codes for the integer representing the power of two, rather than 10 multiplying the fractional number forming the entire real number. In order to accommodate negative powers, offset binary is used. Thus if one considers the set of P logical variables in this field as comprising R_P with the transformation to words Y={y_i,i=1,P} where y_i=x_i+1,i=1,P, the power is decoded as

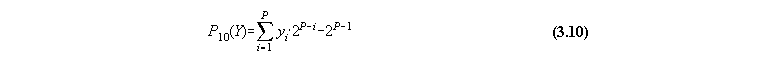
Thus if P=3, the word 011 is decoded as 3-4=-1, and the range of powers accommodated by the set would be -4 to 3 The remaining field forms the mantissa and is interpreted as the fractional field of a binary real number code with the single bit of value 1 preceding. Thus the minimum value which can be coded corresponds to F. This is interpreted as a positive number, MSB=0 with power -2^P-1 and mantissa of decimal number 1. For example if P=8, then the minimum decimal number which can be decoded is 2^-128, or 3.403x10^-38. Notice that in this code the decimal number 0 is represented by this minimum as are all numbers with absolute magnitude less than the minimum. The maximum number which can be represented also depends upon the length of the fractional field, approaching 2¹²⁸ for P=8.

3.7 Double Precision

The term double precision generally refers to a method by which word lengths greater than those corresponding to the register length of a memory location are constructed. This is accomplished by reserving a pair of adjacent memory locations for a single word coding numerical information. Thus if a digital system employs a 16-bit memory, code word lengths of 32 bits may be achieved. One memory location is used to store the most significant 16 bits and the adjacent location is used to store the least significant 16 bits. In this way enhanced precision in the representation of numerical information is achieved although at some cost in complexity. Thus to obtain the information two machine cycles must be employed and the word assembled into a 32 bit accumulator. In principle triple or higher precision could be used. Actually in byte oriented systems what is now accepted as a single precision 16-bit word is assembled from 2 bytes and a double precision word involves 4 bytes.

3.8 Alphanumeric Data

The discussion so far has concentrated upon codes used to represent numerical information. As the very first example showed, a code can be defined for more general information. Alphanumeric information is defined as data in correspondence with the typographical characters. The standard code adopted for this type of information is the ASCII code which uses 7 bit words. Of course for a system with word length greater than 7 the code comprises a subset of the register set with the information contained in the 7 LSB.

3.9 Code specification and transformation

The set of words in the memory of a digital system are classified into the major categories of instructions and data. The definition of a word with respect to these categories is made by memory location in that all those addresses to which the PC may point (directly or indirectly, as will be elaborated upon later) are instructions. The interpretation of words representing instructions is made within the context of the machine instruction code. Data can only be interpreted and manipulated if the corresponding code is specified. At the fundamental level this can be done by assigning sets of addresses to be in association with the codes employed. Thus data in one region of memory could be assigned as binary coded integers, that in another as real numbers represented by the floating point code and so on. In the most general terms the code in effect must be defined for every memory location. Without this step the information in memory is meaningless.

Programs are often prepared with the aid of high level languages designed to facilitate their construction, in particular coding. Data coding may be either explicit or implicit and the details depend upon the language. Examples here will be taken from Fortran. Data are assigned names, which are translated into memory locations, and unless otherwise indicated all data with a name beginning with letters I through N are coded as integers, while all others are coded as real numbers using the floating point representation. This represents implicit coding. It may be overridden by the use of type declarations which are statements indicating the codes to be associated with specific data names. The major data types are integer, real, logical and character, the latter being alphanumeric. In early forms of BASIC only the floating point and ASCII codes were allowed and they were assigned implicitly on the basis of the name used. Alphanumeric data is designated by a name ending with the character $ and referred to as a string. All other data is then treated as real numbers in the floating point type of representation.

Special instructions are included which in some circumstances in effect enable the programmer to perform a code transformation. For example consider a Fortran character variable v. The memory location assigned to v is also defined to interpret the binary word contained therein within the context of the ASCII code. The statement k = ichar(v) however is an instruction to interpret this location in terms of the positive binary integer code. In BASIC the corresponding statement would be k = ASC(v$).